


The purpose of this article is to review the equations for harmonic maps of finite uniton number, in a manner which demonstrates that these equations are integrable in a very strong sense. A more realistic goal is the concept of a completely integrable Hamiltonian system, but many interesting cases are not of this type either. whose solutions can be represented by concrete formulae involving elementary functions of course this goal is usually neither attainable (except in very special cases) nor desirable (concrete formulae are often too complicated to be useful). Since there is, as yet, no universally accepted definition of integrability, the obvious question that arises with any “integrable p.d.e.” is: how integrable is it? Classically, the ideal situation was a p.d.e. It is a relatively recent example, having been recognised as such (by geometers) only in the 1980’s. which can be written as “zero curvature equations”. Guest The harmonic map equation is one amongst many examples of “integrable partial dif- ferential equations”, that is, p.d.e.
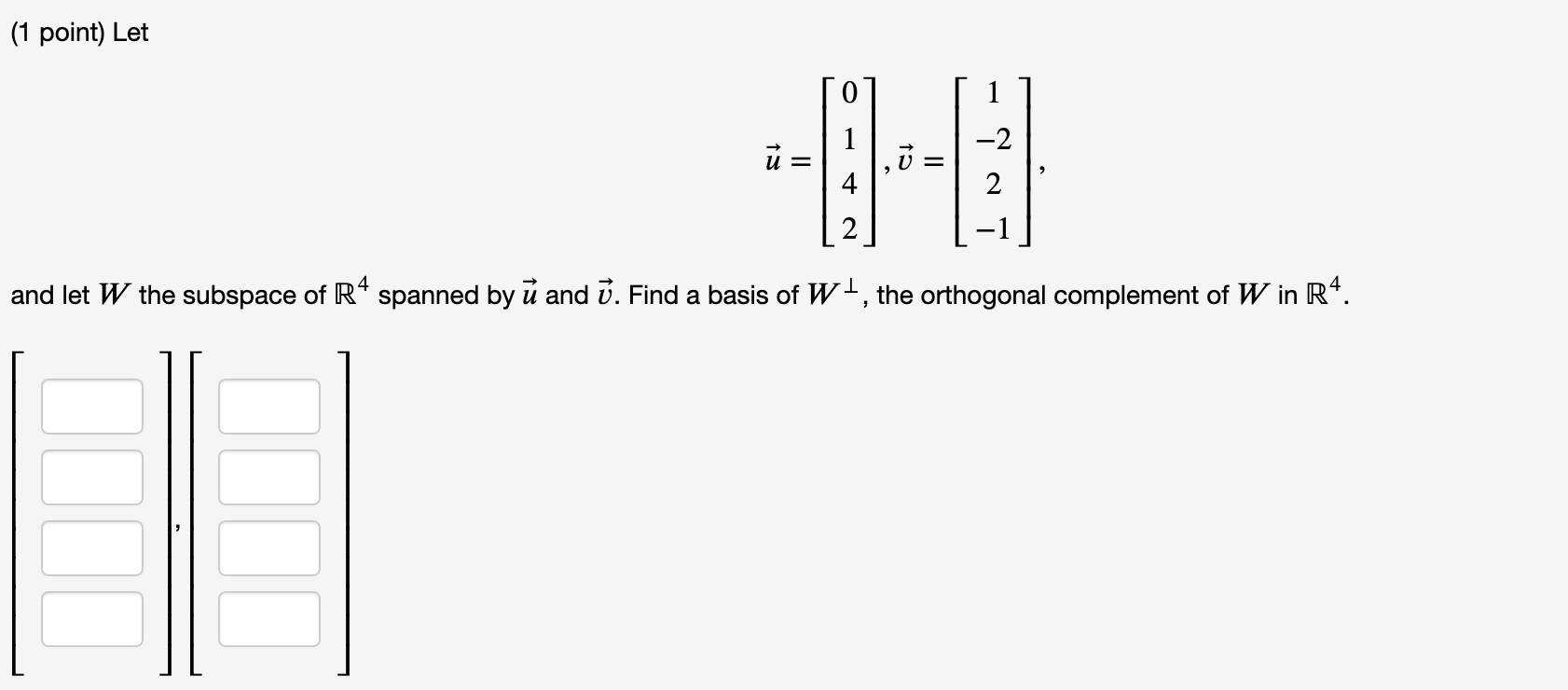
#Complementary subspace definition in math update#
ArXiv:math/0105110v1 AN UPDATE ON HARMONIC MAPS OF FINITE UNITON NUMBER, VIA THE ZERO CURVATURE EQUATION Martin A.


 0 kommentar(er)
0 kommentar(er)
